Trax Tips

Caves can do some very funny things - that is why most people prefer to fill them in. It is often easier not to think about them than be caught by surprise.

You can imagine my surprise when I made the attack on the right (I was white) only to end up losing the game elsewhere to a simple old L. My opponent realised what I did not: I had not actually made an attack! Go on, try it. White cannot complete the loop in one turn.

Suppose Black did try to defend the above attack as shown on the left. The attack certainly looks like it has been defended. On closer look though, this defence has actually made an attack! The white loop may be completed by playing a straight in either of the top two corners of the cave.

Finally, we will consider the Black counter-attack shown here. This illustrates the potential for extending the cave in order to defend an attack. Here we are using what we learned from the first example to know that the white attack is no longer an attack when there is a second black path coming in the bottom. One way of doing this is by attacking.

The attack which isn't really; the defence that didn't but instead made an attack; and the counterattack that doesn't seem to defend, but does. All this is part of the beauty of caves!

Bits for Beginners

A cave is any hollow in the side of the playing area with tiles on 3 or 4 sides.

Caves are an important strategic element in Trax because the sides of the cave restrict what tiles may be played in the cave. This has two important consequences:

• some tile combinations are not able to be played because they don't match the sides of the cave,
• there are more forced moves than usual because of the confined space and restricting nature of the cave walls.

So how do these affect strategy? Well the first point means that some threats which normally work won't in or around caves. In the ultimate, there are dead caves where nothing will work, and no moves are legal. Any path going into such a dead cave cannot be used to form a loop or line.

Just as some threats don't work, some defences don't work either. For example, in the bottom left position, Black is unable to defend the White attack. There is nowhere to turn the White path.

In the bottom right example, the corner on the right foils any defence attempt by resulting in further forced plays which reform the attack! These are the two most common forms of cave attack.

Extras for Experts

Is it possible to determine if a cave is dead? Or if a particular move in the cave is going to be legal?

The answer to the first question is almost. We can determine whether or not a cave can be completely filled. However, this doesn't rule out the possibility of there actually being any legal moves in the cave. In some circumstances we can determine if a particular move will be legal or not, but it is not really any simpler than trying to visualise all the forced tiles.

So how can we tell if a cave can be completely filled? I will use as an example the cave shown on the right. This example is made the more interesting by having both a black and white attack into the cave.

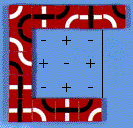
1. Fill the inside the cave boundary with a checker board of + and -. It doesn't matter where you start, just make sure that the pattern is right.
2. Assign each edge inside the cave, the sign of the space it faces into. Add up the total, subtracting the black from the white.
   Here there are 0 +black and 4 -black = -4 black, and there are 3 +white and 2 -white = +1white. Total = +1 - -4 = +5.
3. The cave is only fillable if the absolute value of the total is less than the width of the cave mouth.
   Here 5 > 3 so the cave is not fillable.

Note that this method will only say if the cave in not completely fillable. It says nothing about what may or may not be played within the cave. It is also possible to construct (very contrived) caves where the total is less than the width of the cave boundary and yet the cave still cannot be filled.

A more complete test is to apply the partial test outlined on the previous page to every possible subcave. The full cave is completely fillable only if every subcave is also fillable. If any one subcave is not fillable, then the entire cave obviously cannot be completely filled.

In practise, we can reduce considerably the number of subcaves we need to check. If a subcave has more free edges than edges beside tiles, then the subcaves can always be filled. Based on this we can make the following rules:

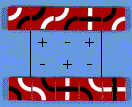
1. In a channel we only need to consider subcaves which are longer than the channel is wide. Here, with a 2 wide channel, we only need to consider subcaves which are 3 or longer.
   In this subcave we have -2 black and +2 white. Total = 2 - -2 = 4. This subcave is therefore fillable.
2. It is only necessary to check subcaves where the free boundaries are the shortest path from one cave wall to another. These minima correspond to straight lines for rectangular caves.
3. Related to this, it is not necessary to check on a 2-sided hollow (in a corner) since such a subcave will have the same number of free edges as edges against tiles, and will always pass the test.
   These rules mean that virtually all subcaves tested will have boundaries directly across a channel. The exception is where there is a complex structure, and the shortest path (minimum) across the structure is not a direct line. I will give an example later.
4. In the back of a 3 sided cave, it is not necessary to check the first two rows / columns. This is because the hollows in the back corner of the cave will always have both a black and a white path going into them (otherwise there would be a forced tile). The black and white path have the same sign so will cancel out.
5. In a complex cave, it is not necessary to check a path immediately adjacent to a hollow. Again, the black and white in the hollow will cancel each other out.
6. Diagonal paths don't need to be checked if the corresponding horizontal and vertical minima have been checked since the number of free edges for the diagonal is the sum of that for the horizontal and vertical paths.
7. For channels one tile wide, only one end of the channel needs to be checked, not every space. Opposite sides of a 1 wide channel must be opposite colours, and therefore cancel out.

To illustrate these rules, I will use a more complex cave example - something that will almost never be encountered across the table. Can this cave be completely filled?
We procede exactly as before in the simpler example. First we place a checker-board of + and - within the cave. The next step is to use the rules to determine which subcaves we need to check, shown here with lines.

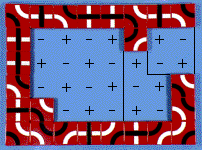
Looking at the innermost subcave:

black: +2 -3 = -1, white: +3 -5 = -2

Total -2 - -1 = -1. Since 1 < 3 this is ok.

Adding the next section on:

black: +3 -4 = -1, white: +5 -6 = -1

Total -1 - -1 = 0. Since 0 < 2 this is ok.

Looking at the complete cave:

black: +4 -4 = 0, white: +7 -7 = 0

Total 0 - 0 = 0. Since 0 < 2 this is ok.

Since all of the subcaves are ok, the complete cave can be filled!

Sidebar: How does it work?

Let the four edges of a tile be labelled t, b, l, r. Let black = 1, white = -1.

The sum of the four edges, t+b+l+r = 0 by definition of the tiles. ie all tiles have 2 exactly black and 2 white edges.

When filling in a region, tiles are placed side by side. By definition, the edges must match. However, we are only interested in the edges around the region, and not any of the internal edges.

For each tile, i within the region to be filled, we have


We get a set of simultaneous equations, one for each tile. from these, we eliminate the internal edges. Consider tile [1] next to tile [2]. If eq[1] is subtracted from eq[2] the internal edge will be eliminated, leaving only the outer edges. With many tiles, the adding and subtracting will give the checkerboard pattern.


If the width of the cave (with no edges) is N, then there are N degrees of freedom (there are N positions which may be either black or white). If the total around the cave boundary is within the range -N to +N then it is possible to arrange a pattern of black and white across the cave mouth to make the total 0.